Aim: Implementing Transposition Cipher( Vernam Cipher)
Theory:
The Verman Cipher :
Verman Cipher is also known as the one‐time‐pad. Gilbert Vernam inventedand patented his cipher in 1917 while working at AT&T. The teletype had been recently introduced, and along with this the commercial Baudot code. Now messages were uniformly thought of as streams of zero’s and one’s. Verman proposed a bit‐wise exclusive or of the message stream with a truly random zero‐one stream which wasshared by sender and recipient.
Example :
SENDING
Message: 0 0 1 0 1 1 0 1 0 1 1 1 …
Pad: 1 0 0 1 1 1 0 0 1 0 1 1 …
XOR ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Cipher: 1 0 1 1 0 0 0 1 1 1 0 0 …
RECEIVING
Cipher: 1 0 1 1 0 0 0 1 1 1 0 0 …
Pad: 1 0 0 1 1 1 0 0 1 0 1 1 …
XOR ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Message: 0 0 1 0 1 1 0 1 0 1 1 1 …
This cipher is unbreakable in a very strong sense. The intuition is that any message can be transformed into any cipher (of the same length) by a pad, and all transformations are equally likely. Given a two letter message, there is a pad which adds to the message to give OK, and another pad which adds to the message to give NO. Since either of these pads are equally likely, the message is equally likely to be OK or NO.
The conclusion that the Verman cipher gives perfect secrecy depends on the assumption that each pad is equally likely. If the pad is used to encipher more than one message, this is no longer true, and the message may be discovered. It is important that a pad once used is discarded. That is the reason for the name one‐timepad, also known as OTP. If this warning is not heeded, the two cipher texts can be subtracted, thus eliminating the pad. What is left is the difference of messages, whichhas a distribution reflecting back on the possibility of choice of pad. This has been
known to completely break the cipher.
The calculation is,
c = m (+) p
and
c’ = m’ (+) p
implies
c (+) c’= (m(+)p) (+) (m'(+)p)= (m(+)m’) (+) (p(+)p) = m (+) m’
The pad has been subtracted off. Although the distribution on pads is uniform, P (p) =1/2n, for any p, the conditional probability of pads given a cipher text, P(p|c), is not. It is exactly the probability of the message being m where m = c (+) p. Given two cipher texts and the understanding that the messages must be plausible for each cipher text under a single pad, we can modify P (p|c) and consequently, P (m|c).
Whether this information is enough to determine the messages and the pads depends on the situation. However, we have violated our absolute requirement for perfect secrecy.
Source Code:
import java.lang.Math;
public class xor {
public static void main(String args[]) {
// This would be the text we encrypt (in this case “hello”)
// We convert it to a character array
String text = new String(“hello”);
char[] arText = text.toCharArray();
// This would be our vernam cipher (should be same length as ourtext)
// Here we use the same letters, but theoretically should be random
// characters generated on the fly. USE RANDOM LETTERSs
String cipher = new String(“XYZHG”);
char[] arCipher = cipher.toCharArray();
// Array to hold our encryption (again same length)
char[] encoded = new char[5];
// Encrypt the text by using XOR (exclusive OR) each character
// of our text against cipher.
System.out.println(“Encoded ” + text + ” to be… “);
for (int i = 0; i < arText.length; i++) {
encoded[i] = (char) (arText[i] ^ arCipher[i]);
System.out.print(encoded[i]);
}
System.out.println(“\nDecoded to be… “);
// Run through the encrypted text and against the cipher again
// This decrypts the text.
for (int i = 0; i < encoded.length; i++) {
char temp = (char) (encoded[i] ^ arCipher[i]);
System.out.print(temp);
}
}
}
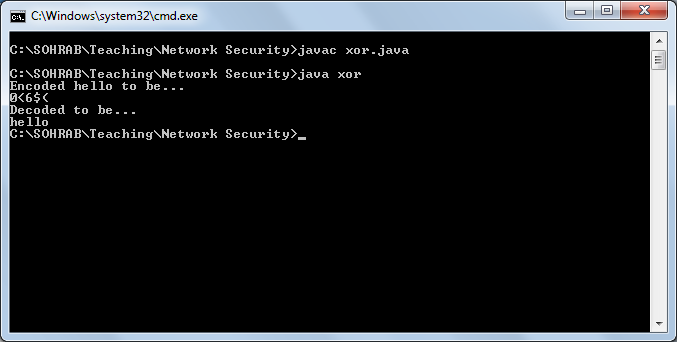
Output: